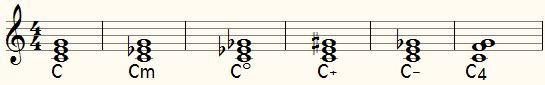Chords and music theory
As soon as you want to do a bit more with music than just playing, it is very useful to know a bit about music theory. The following section tries to provide as much information that terms such as key, tonality, minor, major, chords, chord progressions, intervals, circle of fifths, will get a bit more meaningful. Clearly written sheet music (with chord symbols and accompaniment parts generated therefrom) as provided using music notation program MusiCAD, greatly helps in the understanding of music theory in practice.
Playing with music
To make music theory more accessible it is extremely important that you can hear what chords do to a melody. If you are an excellent piano player, you may be able to get by with information and examples on paper (or the web). If you play a non-chord instrument (all wind instruments, violin, cello, etc.) and/or don't play from sheet without any problems, it makes a lot of sense to use a sheet music program with extensive support for working with chord symbols to get some grip on harmony usage.
If a piece of music contains chord symbols, you can automatically play a number of accompaniment parts based on the chord symbols, for which the chord symbols and the time signature form the basis. By entering (part of) a piece of music and using the information provided here to 'play' with chords, you will quickly gain more insight into your music's harmony and you will be able to enjoy it more.
Depending on the instrument you play or for which you write parts, you will have to take into account the (im)possibilities of the instrument: transposition and range (trumpet, clarinet, tuba) chord diagrams for guitar, ukulele, mandolin, banjo etc.
Of course you can have a double bass part played by a soprano recorder - select another clef and a few octaves up - but that is usually not a really good idea. If you know a bit about the how and why of chords you will be able to make much more suitable parts.
Download and install (no cost, no time limit) and use the program along with the information given here to go from just reproducing notes through playing with music to make music.
Musical distances - frequently used terms
Every two tones have a mutual relationship that has to do with the ratio of their pitches. In most music, the most important ratio is the "octave". The octave is the relationship between two tones where the frequency of one tone is exactly twice as high as the other. On stringed instruments this can be illustrated by looking at what happens when a string is divided into two equal parts using a finger. The pitch between the string when it is sounded full length and the string when it is split in two by a finger is exactly one octave. Likewise, such a half string can again be divided in two, with which there is again an octave between the half and the quarter string. Between the frequency of the whole and the fourth string there is a relation of 1:4, so two octaves or a double octave.
Musical distances that can be expressed in octaves sound easy to our ear. In fact, it's sometimes hard to tell whether two notes are the same height (also called "unison") or whether they have an octave relationship, especially when played by different instruments.
Consonant, dissonant or simply out of tune...
The degree to which the ear perceives a musical distance (interval) between two simultaneously sounding tones as pleasant is often referred to as "consonant", while a pitch that "twists" is indicated by the term " dissonant" (non-consonant). "Out of tune" we call intervals that are not pure, i.e., not a multiple of semitones. Inexperienced listeners will often confuse dissonance and out of tune, an interval b-c or a semitone they call out of tune while this is only very dissonant. In music performance, such a dissonant interval occurs often, while an interval out of tune (hopefully) never occurs (experimental music aside for the time being).
Over the centuries a musical scale has been developed which divides the octave into 12 equal parts, called semitones.
For historical reasons some other tone distances were given their own names. The naming can be found on the piano, start at middle C and going all the way up using the white keys to the right: prime, second, third, fourth, fifth, sixth, seventh and octave. A series of tones that always a semitone apart is called a chromatic series (white and black on piano), in contrast to a diatonic series as the white keys on the piano.
Tone scale
Over the centuries, a musical scale has been developed that divides the octave into 12 musically equal parts, called semitones. A distance of two semitones is called a "whole tone".
For historical reasons, which will be discussed in more detail later when discussing scales, a number of other tonal distances have also been given their own names. The names can be found on the piano: start on middle C and go one white key to the right. second, third, quarter, fifth, sixth and seventh. The eighth is once again a C, but an octave higher.
The terms major and minor mainly refer to the first third in the scale, for example, major third is the distance between the note c and the note e . A minor third is the distance between the note c and the note eb. The seventh is also available as minor seventh (c - bb) and major seventh (c - b).
The term diminished indicates a semitone decrease, while augmented indicate a semitone increase.
A sequence of notes spaced half a note apart is called a “chromatic” sequence (white and black on piano), as opposed to a “diatonic” sequence like the white keys on the piano.
Naming of tones
In addition to naming tone distances, the naming of pitch height has also arisen. Seven letters were chosen for this a few centuries ago: A-G. In times when the computer had not yet made its entrance, octaves were designated 'large', 'small' and 'striped'. For calculation purposes, indications with an octave number are more practical. Usually the note A4 serves as a reference, or the A above middle C on the piano. This A4, the pitch of most tuning forks, usually has a frequency of 440 Hz (440 vibrations per second). All other tones are derived from this. An A6 is therefore two octaves higher than an A4. The naming of a chromatic series is now as follows:
A - A#/B♭ - B - C - C#/D♭ - D - D#/E♭ - E - F - F#/G♭ - G - G#/A♭ A
A # after a letter is called a sharp and indicates that the pitch has been raised by a semitone, while a ♭ (often written as a lowercase b for convenience ) called a flat and indicates that the tone should be lowered by a semitone. When looking at the black keys of a piano it comes to mind that more than one name might be used for them. An A# and a B♭ sound the same (on piano) but have different names. The difference in naming is due to the function that a note has within a melody, and is called enharmonic exchange (a violinist might play a slightly different pitch!). If the tone A#/B♭ acts as a lowered B, then it is notated as B♭, and if the function is that of a raised A then it will be noted as an A#. Also the usually "simple" notated notes can be given an alternative notation; a B that is used as a lowered C can be written as C♭, as can a C used as a raised B might be notated as B#.
It can also sometimes happen that in a melody the tone G# occurs, for example, as the root, while in addition there is also a raised G#. This raised G# (double sharp G) can now be written as G##, and sounds (on a piano) like an A. To keep music legible, double sharps and flats will not be written very often...
Every note (except the G#/A♭) can therefore be 'spelled' in three ways.
Scales
A scale forms the basis of any melody (excluding atonal music). Starting from a scale that repeats itself after an octave, we again divide the octave into a number of parts. Our ear's preference for consonant proportions has resulted in a sequence of eight notes that looks like this:
Prime, Second, Third, Quarter, Fifth, Sixth, Seventh, Octave. Such a series of tones is called a "diatonic" scale because of the lack of a number of (semi) tones. Each note of that scale thus has a fixed relationship with the first note of that scale, often indicated by the aforementioned name in Latin.
Let's take the scale of C as an example: C-D-E-F-G-A-B-C. On the piano this comes down to 8 adjacent white keys from C. The note pattern looks like the figure below.
C D E F G A B C
So far pretty straight forward, but what happens if you don't start on the C but on an A?
A-B-C-D-E-F-G-A has a very different scale as a scale than C-D-E-F-G-A-B-C although they use exactly the same notes. The difference is in the distances, although you don't even see that on a staff:
A B C D E F G A
Between a B and C resp. E and F a pitch of a semitone while between all the others there is a pitch of a whole tone (two semitones). Not all steps of the ladder have the same size! The first scale is called a "major" scale, the second a "minor" scale. A scale can also be built on the other tones, but most of them sound strange to most people. Assume that we want to keep the 'character' of the scale, but make everything sound a whole note higher. What needs to be done is to keep the distances the same as with the described scale of C. For this the F and C have to be raised by a semitone, and we now get a scale notated with two sharps. In the notation, these 'sharps' (a hashtag-like symbol) are written in front of each line to indicate that they are tonal to the scale as opposed to notes used in a melody accidentally be raised/lowered.
D E F# G A B C# D
In a major scale, the distance between the 3rd and 4th steps of the scale, and those between the 7th and 8th steps will always be a semitone, while the distance between the other steps will be a whole.
Now let's compare the minor scale of D with the major scale of D:
Both note images look exactly the same (except for the accidentals), but sound very different!
Let's take a look at distances between notes. The first thing you notice is the difference in distance between the root and the third stage. For the major scale that is two whole tones, while for the minor scale it's a whole plus a semitone. It is now said that the distance from the first to third stage is a major third for the major or major third scale, while that in the minor scale is a minor third, and is therefore also called a minor third scale. .
So with each scale belong a number of flats or cross; except for the scales of C major and A minor (Am) which are written without sharps or flats. The scales of A minor and C major are called each other's "parallel" because of the same accidentals, so A minor is the parallel minor scale of C major. The same goes for, for example, D minor and F major, both with a flat. For example, each of the twelve major scales always has a parallel minor scale that starts a minor third lower. Parallel scales are often used interchangeably within a melody.
Chords
Chords in their simplest form are triads and therefore consist of at least three notes that can be heard simultaneously. A melody can usually be accompanied by chords in a simple way. From the chords a bass part can be found, second voices etc.
Major
Chords and scales have a very direct relationship; from the scale used often immediately follow the chords to be used and vice versa. If we once again introduce the scale of C major, we can see how triads can be found in that scale. In order to sound good in a key, a triad must be built up from tones that occur in the scale or that are 'proper'. A second limitation we find for easy-to-hear chords is that chord notes cannot be next to each other.
By building a triad on every step of the scale (always skipping one step) we find 7 triads, which we now indicate with a Roman numeral for the degree (step of the scale) on which the chord started (relative chord notation relative to key). The triads found, however, do not all have the same character: on I IV and V the chords sound major (major), they are made up of a major third with a minor third stacked on top. Such major chords are often notated in music with capital letters: C F and G for I IV and V in C major (chords in letters independent of the key).
On II III and VI we can find three minor (minor) chords, a minor third with a major third on top. Minor chords are written with the uppercase root of the chord followed by a lowercase letter m. Am, Em and Dm for resp. VI, III and II in C major.
One chord does not belong in either category: on VII there is a diminished chord, made up of two minor thirds. Diminished chords are notated with the letter of the chord followed by a small zero slightly higher: Bo or sometimes as Bdim. They are much less common than the minor and major chords and are not considered here.
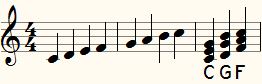
After some fiddling with the above chords, it is noticeable that with the three major chords C G and F the entire scale can be covered, as it were. The same goes for the three minor chords Am Em and Dm. It seems obvious to accompany melodies with a set of three chords as described here.
In addition to three, chords can also consist of four or more different notes (notes that are one octave apart are considered "equal" here). However, there is only one such chord that is also very easy to listen to. Combining the unused VII chord with the V chord results in what is called a "seventh" chord and is written as G7 because the extra F in this chord is the (decreased) seventh note. from the scale of G (decreased because the scale of G normally contains an F# and no F).
What's the use of such a seventh chord? It turns out that when such a seventh chord is played it calls up "tension", asks a question, which can be solved by playing another chord. The chord that best answers the question of the available 7 options is the chord on the root, in this case the C chord.
Just a little bit of slang, the chords on the stairs have alternative, commonly used functional names.
| I | Tonic |
| II | Super-tonic |
| III | Mediant |
| IV | Sub-dominant |
| V | Dominant |
| VI | Sub-mediant |
| VII | Sub-tonic |
Minor
With minor scales a complication arises from our otherwise fairly simple model of the theory of harmony that we are actually working on. What's the problem?
For a major scale, we had found two chords that were very strongly linked: the Dominant-seventh chord, which asks, as it were, for the Tonic chord.
But what causes that demand effect now. It turns out that half-note distances exert a strong attraction. In the major scale, there is a semitone distance on the third and seventh steps. The chord transition from G7 to C uses both semitones; f→e and b→c.
If we add the minor scale and also admire the chords on I V7 and IV, we find Am, Em7 and Dm. We have now unfortunately lost a semitone jump at the transition from Em7 to Am, while the remaining b→c does not pull nearly as effectively; in C major this transition strongly moved to the tonic, while in A minor this is not the case (after all, the note c is not the root note here...)
We do have a solution for this, but we immediately introduce a new kind of scale... If instead of the 'ordinary'; seventh stage use a raised seventh stage in the scale (a g# instead of a g) then we create an extra half-step g# → a, yes the pulling-note we were looking for. The price we pay for this is an interval of three semitones between f and g#. This can sometimes sound a bit exotic. The scale is called the "harmonic" minor scale.
A remedy for that large step is also raising the 6th stage. That would mean that the subdominant chord would also become major... The ultimate remedy for this dilemma is to raise VI and VII "if necessary" so when a transition E7 → Am occurs: the resulting scale is usually referred to as a melodic minor scale: ascending with f# g#, descending with g f.
We arrived at the major and minor scales by starting on the white keys of the piano at c and a respectively, resulting in very different sounding scales. A regularly occurring alternative is the scale that starts on d. For comparison with the earlier scales transposed to A, this gives the Doric minor scale:
A very well-known example of a music in a Dorian ladder is for example "The drunken sailor". The crucial differences in character between the different scales are caused by the position of the half-steps in the scales.
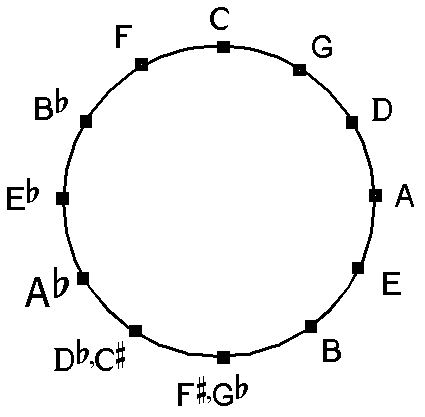
The circle of fifths
With the so-called circle of fifths a large number of music-theoretical matters can be placed in a manageable framework. Nice, but what is that...
If you start with a C and go up a fifth (=7 semitones) you get the following sequence:
C - G - D - A - E - B - F# - C# -G# - E♭ - B♭ - F - C
With the C in the middle, above it we get the number of sharps or flats that belong to the corresponding major and minor keys:
| sharps/flats | 7♭ | 6♭ | 5♭ | 4♭ | 3♭ | 2♭ | 1♭ | - | 1# | 2# | 3# | 4# | 5# | 6# | 7# |
| major | C♭ | G♭ | D♭ | A♭ | E♭ | B♭ | F | C | G | D | A | E | B | F# | C# |
| minor | A♭m | E♭m | B♭m | Fm | Cm | Gm | Dm | Am | Am | Bm | F#m | C#m | G#m | D#m | A#m |
It is immediately noticeable that in minor and major scales with the same root note (C and Cm for example) three flats more / sharps less must be notated.
Since the f# and g♭ on piano are the same, this sequence can also be drawn in the form of a circle: the circle of fifths.
If the C is at the top, each step clockwise represents one sharp for the scale or a flat off, while each step counterclockwise represents a sharp off or a flat. So the scale of E♭-major has 3 flats, that of B-major has 5 sharps etc.
Find chords to a melody
Finding chords to a melody requires some practice and especially good ears! Here are a few 'hints' to quickly find chords to a given melody.
1) Find out in which key the melody is (or should be). The most obvious possibility is the note with which the melody starts and/or ends (about 75% chance). In case of an pickup: look at the first note of the first 'true' bar.
2) Determine whether the melody has a minor ('sad') or major ('happy') feel.
3) If in 1) for example a G was found and in 2) 'sad', then the key is G-minor (Gm) and therefore has (as can be found in the previous table) two flats as a sign. Likewise A and 'happy' gives A major (A) and thus 3 systematic sharps.
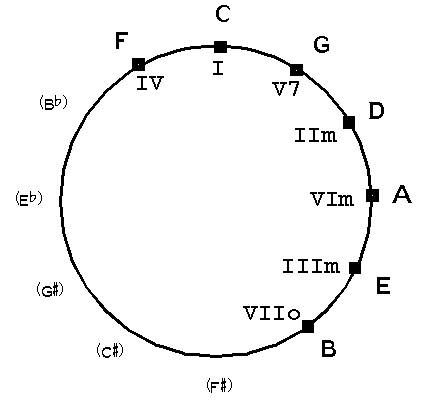
4) The key now largely determines which chords can be used. We had already seen which chords are most obvious in a scale: I, V7 and IV. We can easily find these using the circle of fifths. Look on the circle of fifths at the notes that are to the left and right of the root of the scale. These are exactly the IV, I and V chord with the chord that has the same name as the scale in the middle. The most commonly used chord is the tonic chord or the chord that has the same name as the scale itself. The second important chord is the chord on the circle of fifths to the right of the tonic. This chord is called a "dominant" chord because it dominates the scale. The dominant seventh chord is also the only major chord that is proper with a seventh scale. So for C major we have as chords:
C G7 and F as base and Am Em Dm and Bo for variety. In MusiCAD you can use the chord wizard to help you figure out the accompaniment chords.
5) Begin accompanying a melody with the chord on the tonic. If this doesn't sound anymore, try the dominant (or dominant seventh chord). If this doesn't sound either, try the sub-dominant chord (so in C major they become: C G7 and F, or in A minor Am E7 and Dm.)
6) If an I-V7-IV accompaniment is not sufficient, you can use the circle of fifths to find some extra possible chords; to the right of the IV-I-V7 trio are still IIm, VIm and IIIm or III7 available. In the circle of fifths shown, the tonic (=I) is C. The scale is marked on the circle.
For keys other than C (or Am), the contents of the circle of fifths can, as it were, be rotated to find the right chords: make sure that I is next to the key, and all chords belonging to the key can be read.
| IV | I | V7 | IIm | VIm | IIIm | VIIo | ||
| E flat major | ♭♭♭ | A♭ | Eb | B♭7 | Fm | Cm | Gm | Do |
| B flat major | ♭♭ | E♭ | B♭ | F7 | Cm | Gm | dm | Ao |
| F major | ♭ | Bb | F | C7 | Gm | Dm | Am | Eo |
| C major | F | C | G7 | Dm | Am | Em | Bo | |
| G major | # | C | G | D7 | Am | Em | Bm | F#o |
| D major | ## | G | D | A7 | Em | Bm | F#m | C#o |
| A major | ### | D | A | E7 | Bm | F#m | C#m | G#o |
| IVm | Im | V7 | II | VI | III | VII | ||
| C minor | bbb | Fm | Cm | G7 | Do | Ab | Eb | Bb7 |
| G minor | bb | Cm | Gm | D7 | Ao | low tide | Bb | F7 |
| D minor | b | Gm | Dm | A7 | Eo | Bb | F7 | |
| A minor | Dm | Am | E7 | Bo | F | C | G7 | |
| E-minor | # | Am | Em | B7 | F#o | C | G | D7 |
| B minor | ## | Em | Bm | F#7 | C#o | G | D | A7 |
| F-sharp minor | ### | Bm | F#m | C#7 | G#o | D | A | E7 |
One of the most important things to remember from this story about scales is: "semitones pull". If you use half-steps in the right places (and the corresponding chords) in a melody (or second voice), you pull the melody forward. In the circle of fifths you will always find the semitones on the third and seventh steps of every seventh chord.
Just play B7 - E7 - A7 - D7 - G 7 - C, - a piece of the circle of fifths - and you hear a very compelling series of semitone steps.
In such a series of seventh chords you can even find a third semitone distance at every chord transition e.g. with B7-E7 there is except d#-d and a-g# you can also listen to d#-e. In the closing transition G7-C you now omit the seventh (the b♭), so that the compulsion to yet another chord remains; we're back home (assuming we're playing in C major).
Notation and use of 'difficult' chords.
If you browse through sheet music that uses chord symbols, you will notice that some more complicated chords are used such as C6, C9, C+, C4, CmΔ etc. Once you know how the standard chords are constructed, it's not that hard to figure out how the extended chords fit together.
In the earlier story you noticed that the emphasis has been very much on scale own chords. As in-scale triads (chords with three notes) you have seen three types of chords:
- major: major third ( C: c-e-g )
- minor: minor third ( Cm: c-e♭-g )
- diminished: two minor thirds: ( Co or Cdim: c-e♭-g♭ )
The remaining possibility is:
- augmented: two major thirds ( C+ or Caug: c-e-g# )
Of some importance are some outliers (not consisting of major or minor thirds):
- suspended 2nd: hard lowered 3: (C2 or Csus2: c-e♭♭-g or c-d-g )
- suspended 4th: augmented 3: (C4 or Csus4: c-e#-g or c-f-g)
- hard diminished: major third + lowered 5 (C-, C(♭5) C(-5) : c-e-g♭)
If you expand the now known triads with an extra third, you get the seventh chords, the most important of which are:
extension with minor third
| C7 | c-e-g-b♭ | dominant seventh | |
| Cm7 | c-e♭-g-b♭ | minor seventh | |
| Co | c-e♭-g♭-b♭♭ | diminished-seventh | (also Co7, Cdim, Cdim7) |
That last note of the diminished seventh chord (the b♭♭, double flat b) is often rewritten as a - making the third spacing somewhat unclear: g♭ - a no longer looks like a third but as wide second g♭-a. Usually an a is written in order to avoid difficult to read double flats that do not result in a different playing style on many instruments.
Major third expansion
| CΔ | c-e-g-b | major seventh | (also CM7, CMaj7) |
| CmΔ | c-e♭-g-b | minor-major-seventh | (also CmM7, CmMaj7) |
| Cø | c-eb-gb-b♭ | half-diminished-seventh | (also Cm7(♭5)) |
Another third gives the so-called ninth chords:
| C9 | c-e-g-b♭-d | dominant-ninth |
| Cm9 | c-e♭-g-b♭-d | minor-ninth |
Note that expanding a diminished seventh chord with another minor triad does not produce a 'new' chord; the root note is added again. Further stacking of thirds upon a major or minor chord successively produces "undecime"; (or "eleventh") and "tredecime"; ("thirteenth") chords, the most common of which are:
| Cm11 | c-e♭-g-b♭-d-f# | minor-eleventh |
| C13 | c-e-g-b♭-d-f#-a | thirteenth |
In this last C13 playing the 'thirteen' one octave lower produces an 'added sixth' chord:
| C6 | c-e-g-a | sixth |
| Cm6 | c-e♭-g-a | minor-sixth |
These last two chords (often within scale) are used quite a lot. Also the omission of notes happens a lot; a C9 is often played as c-e-g-d.
We have already seen that for convenience single notes can be enharmonic exchanged. The same can happen with chords. A chord consisting of g#-b-d-f can be equally justifiably be named a G#ochord as an A♭o chord (g# = a♭) There is even more going on with these diminished seventh chords. A Bo chord consists of b-d-f-g# and thus of the same notes as G#o. Also Do and Fo are enharmonic interchanges of this same chord.
In fact, there are only three substantially different diminished seventh chords:
| Co | = | E♭o | = | F#o | = | Ao | also D#o resp. G♭o |
| C#o | = | Eo | = | Go | = | A#o | also D♭o resp. B♭o |
| Do | = | Fo | = | G#o | = | Bo | also A♭o |
Something similar can be found with augmented or augmented chords:
| C+ | = | E+ | = | G#+ |
| C#+ | = | F+ | = | A+ |
| D+ | = | F#+ | = | A#+ |
| E♭+ | = | G+ | = | B+ |
Then there are chords that suddenly form another chord in a different position:
| I6 | = | VIm7 | : | C6 | : | c-e-g-a | = | Am7 | : | a-c-e-g |
| IIm6 | = | VIIø | : | Dm6 | : | d-f-a-b | = | Bø | : | b-d-f-a |
A chord example
The piece above has a lot of chords added. Using the rules as we had set up earlier, there would have been much less chords; C | G7 | G7 | C | C | G7 | G7| C | would have done.
Diminished chords can often be referred to as "passage chord" to use; in the next section, a diminished chord is used to move up a whole note in your chord line. If you want to go from C to Dm, you can now use the C#° chord as an intermediate step. G to Am ditto with G#°, as well as F to G with the F#° chord as well.
In chord progressions as they are used in practice, the restriction that chords must be scaled-proper is usually not strictly applicable. Using strange chords in the right place can create the atmosphere you need when arranging a melody.
An augmented chord in the major scale can never exist in-scale; none of the major chords can be augmented using in-scale notes only. E.g. in C major: C+ gets an out-of-scale g#, G+ gets a d#, and F+ a c#. When can you use such an augmented chord? An example use may be as a replacement for the dominant-seventh chord (provided the melody allows for this). Usually to go from G to C you use the G7 chord with the pulling notes b (to c) and the f (to e). It is also possible with a G+ chord; the out-of-scale d# pulls to the in-scale e.
The use of major-seventh chords often mean that the harmony remains "floating". The presence of both a 'c' and a 'b' in for example a CΔ seems to cancel each other's effect. The c pulls (in-scale) to b. The b pulls to c. In other words, even if the request is fulfilled, the tension is still not gone. Note that major-seventh chord containing only notes from the scale can be used on both I and IV (in C: CΔ and FΔ). Minor-major-seventh chords are usually not scaled; only AmΔ is in-scale in Am in melodic/harmonic variant. In the original minor scale (without a raised seventh), all minor-major-seventh chords are out-of-scale.
Chord positions
You can construct chords in different positions; after all, a C chord consists of c-e-g and can be played as c-e-g (root position), e-g-c and g-c-e. More complicated chords in particular do not sound equally useful in all positions; the notes you want to stand out should be as high up in the chord as possible. C7 played as b♭-c-e-g "wrings" more than c-e-g-b♭ (because of the second b♭-c) the latter also resolves more emphatically to F: c-f-a both leading tones e-f and b♭ -a are as high as possible. c-e-g-b♭ to f-a-c is much less emphatic.
You can also have (three or more) wind instrument players play long chord notes as accompaniment parts.
Common chord progressions
A few common chord progressions, all in C resp. Am:
| C F G7 C | (final) cadence (I-IV-V7-I) |
| Am Dm E7 Am | ditto minor (Im-IVm-V7-Im) |
| C G F C | plagal cadence (IV-I instead of V-I as final chords) |
| Am E7 A | picardic third (Im-V7-I) |
| C Dm G7 C | authentic cadence (I-IIm-V7-I) |
| Am G F E7 | Andalusian Cadence (Im VII VI V7) |
| C D7 G7 C | intermediate dominant (trip to higher key) |
| Am B7 E7 Am | same minor. |
| C F Fm C | minor IV (ladder strange) |
| C C7 A A7 Dm G7 C | major III |
| C C#o Dm | passing chord (semitones in the bass) |
| G G+ C | as a replacement for G7 C |